Effects of taxes and subsidies on markets:calculations (HL only)
In this section, we will engage in numerical analysis of the effects of a tax and a subsidy on markets and the stakeholders involved.
Tax
The government of Economica realises that smoking is fast becoming a menace in the country. Smoking not only affects the health of the smoker but also creates costs for third parties or the people who are exposed to secondhand smoke. The government has implemented a suite of policy measures to deal with the problem of smoking. The most important of these measures is a 5 Nom per pack specific tax imposed throughout the country. The diagram below shows the market for cigarettes after the tax.
Let us use the information provided on the diagram to calculate the following after the imposition of the tax:
-
the change in price
-
the change in quantity sold
-
the change in consumers' expenditure on cigarettes
-
the change in producers' revenue
-
the government's tax revenue from cigarettes
-
the change in consumer surplus
-
the change in producer surplus
-
the deadweight loss
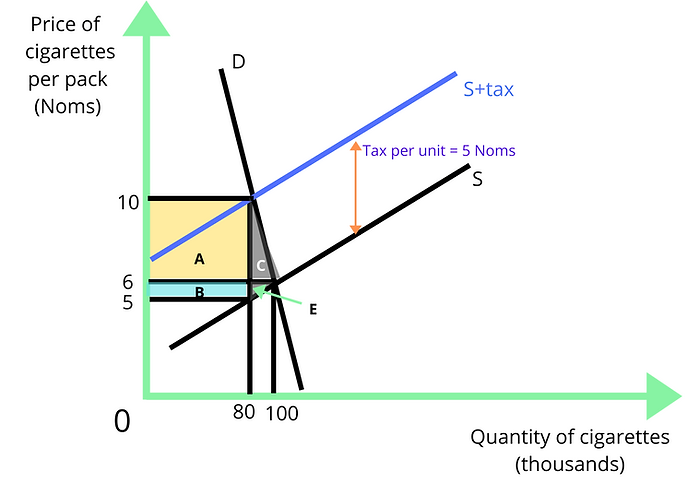
Looking at the diagram, we can see the equilibrium price on the free market was 6 Noms while the price increases to 10 Noms per pack after the tax. The change in price is therefore 4 Noms per pack.
The number of packs sold on the free market was 100,000 which has now decreased to 80,000 due to the increase in price as a result of the tax. The number of cigarette packs sold has fallen by 20,000 as a result of the tax.
The consumers' expenditure on cigarettes initially was P*Q = 6 * 100000 = 600,000 Noms.
The consumers' expenditure after the tax is P*Q = 10 * 80000 = 800,000 Noms.
The change in consumers' expenditure = New consumers' expenditure - initial consumers' expenditure = 800,000 - 600,000 = 200,000 or a rise of 200,000 Noms.
The producers' revenue from the sale of cigarettes initially was P*Q = 6 * 100000 = 600,000 Noms. After the tax is imposed, the price per pack is 10 Noms. An amount of 5 Noms per pack is paid to the government. Therefore, the price received by the producers per pack is 5 Noms. The producers' income after the tax is P*Q = 5 * 80,000 = 400,000 Noms.
The change in total revenue = New total revenue - initial total income = 400,000 - 600,000 = 200,000 or a decrease of 200,000 Noms.
The tax per unit is 5 Noms. In the post-tax equilibrium, 80,000 packs are sold. The government's revenue from the tax is therefore 5 * 80,000 = 400,000 Noms.
From the diagram, we can see that the lost consumer surplus is represented by the areas A and C as the consumers pay a higher price of 10 Noms per pack.
Area A = length * width (area of a rectangle)
= 4 * 80000
= 320,000 Noms.
Area C = 1 * base * height (area of a triangle)
2
= 1 * 20,000 * 4
2
= 40,000 Noms
Lost consumer surplus = Area A + Area C = 320,000 + 40,000 = 360,000
The consumer welfare is reduced by 360,000 Noms.
Similarly, areas B and E represent the loss in producer surplus as the producers receive a lower price of 5 Noms per unit.
Area B = length * width (area of a rectangle)
= 1 * 80,000
= 80,000 Noms
Area E = 1 * base * height (area of a triangle)
2
= 1 * 20,000 * 1
2
= 10,000 Noms
Lost producer surplus = Area B + Area E = 80,000 + 10, 000 = 90,000
The producer welfare is reduced by 90,000 Noms.
Area C represents lost consumer surplus that is not regained by another group and so it is a deadweight loss. Likewise, area D represents lost producer surplus that is not regained by another group.
Deadweight loss = Area C + Area E
Area C = 40,000 (calculated above)
Area E = 10,000 (calculated above)
Deadweight loss = 50,000 Noms
Subsidy
The government of Economica decides to use the money raised through taxes to provide a subsidy for health care. The diagram below shows the market for hospital beds in the country after the subsidy.
With reference to the diagram, let us calculate the following after a subsidy of 90 Noms per unit has been granted:
-
the change in price
-
the change in quantity sold
-
the change in consumers' expenditure
-
the change in producers' revenue
-
the government's expenditure on the subsidy
-
the change in consumer surplus
-
the change in producer surplus
-
the deadweight loss
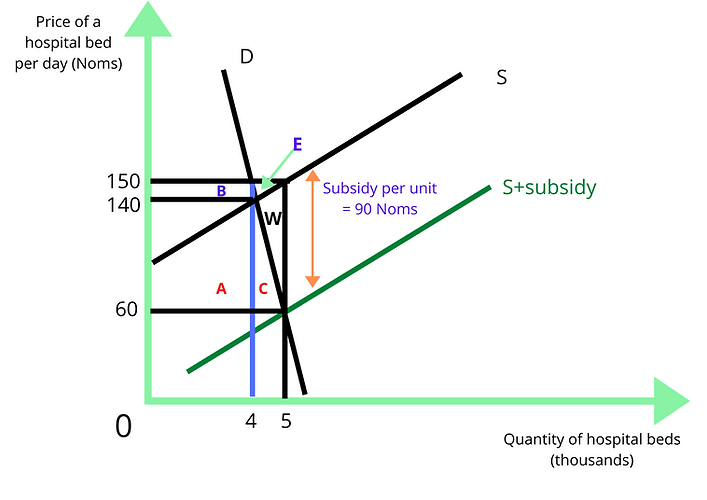
Looking at the diagram, we can see the equilibrium price on the free market was 140 Noms while the price falls to 60 Noms per bed. The change in price is therefore 80 Noms per bed.
The number of beds consumed before the subsidy was 4,000 which has now increased to 5,000 due to the fall in price as a result of the subsidy. The number of hospital beds consumed has therefore increased by 1,000.
The consumers' expenditure on hospital beds initially was P*Q = 140 * 4,000 = 560,000 Noms.
The consumers' expenditure after the tax is P*Q = 60 * 5,000 = 300,000 Noms.
The change in consumers' expenditure = New consumers' expenditure - initial consumers' expenditure = 560,000 - 300,000 = 260,000 or a fall of 260,000 Noms. The consumers are spending 260,000 fewer Noms and able to consume a larger quantity.
The producers' revenue from the sale of the service (hospital beds) initially was P*Q = 140 * 4,000 = 560,000 Noms.
After the subsidy is granted, the producers receive 60 Noms from the consumers as the price. In addition, the government pays a subsidy of 90 Noms for every unit. Thus, the total price received by the producers for each unit is 150 (= 60 + 90) Noms. The producers' income after the subsidy is P*Q = 150 * 5000 = 750,000 Noms.
The change in total revenue = New total revenue - initial total income = 750,000 - 560,000 = 190,000 or an increase of 190,000 Noms.
The subsidy per unit is 90 Noms. In the post-tax equilibrium, the quantity consumed is 5,000. The government's expenditure on the subsidy is therefore 90 * 5,000 = 4,50,000 Noms.
From the diagram, we can see that the consumers gain areas A and C as a result of the subsidy, This is because the price falls to 60 Noms.
Area A = length * width (area of a rectangle)
= 80 * 4000
= 320,000 Noms.
Area C = 1 * base * height (area of a triangle)
2
= 1 * 1000* 80
2
= 40,000 Noms
Gain in consumer surplus = Area A + Area C = 320,000 + 40,000 = 360,000 Noms.
The consumer welfare is increased by 360,000 Noms
Similarly, areas B and E represent the gain in producer surplus as the producers receive a higher price of 150 Noms per unit.
Area B = length * width (area of a rectangle)
= 10 * 4000
= 40,000 Noms
Area E = 1 * base * height (area of a triangle)
2
= 1 * 1,000 * 10
2
= 5,000 Noms
Gain in producer surplus = Area B + Area E = 40,000 + 5, 000 = 45,000 Noms.
The producer welfare is increased by 45,000 Noms.
We can calculate deadweight loss in two ways. The first would be to calculate the deadweight loss directly as area W.
Area W = 1 * base * height (area of a triangle)
2
= 1 * 1000* 90
2
= 45,000 Noms
Alternatively, deadweight loss can be calculated as the difference between the government's expenditure on the subsidy and the increase in societal welfare as measured by the sum of consumer and producer surplus (or community surplus).
Consumer surplus + producer surplus = 360,000 + 45,000 = 405,000 Noms
Government's expenditure on the subsidy = 450,000 Noms
Deadweight loss = Government expenditure on the subsidy - increase in community surplus
= 450,000 - 405,000 Noms
= 45,000 Noms
.png)